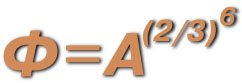

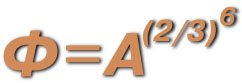 |  |
Автор - Гладков Борис Васильевич, член Международной Петровской Академии наук и искусств, к.т.н., заведующий кафедрой Методологии Познания Университета Экологии Искусства. Автор ряда изобретений в области электромеханических и акустических устройств. Разработчик теории Сферодинамики.
| КАТЕГОРИИ МИРОВОЗРЕНИЯ КАК МЕТОД ПОЗНАНИЯ Положение о том, что пространство и время представляют собой способ познания вещей человеком было установлено и блестяще обосновано великим немецким философом Иммануилом Кантом. Понятия пространство и мировоззрение адекватны, и этот вопрос был прекрасно разработан долго замалчивавшимся выдающимся российским космистом Петром Демьяновичем Успенским, который в своей книге TERTIUM ORGANUM КЛЮЧ К ЗАГАДКАМ МИРА, С.Петербург, 1904 г. обосновал четыре категории человеческого мировоззрения. И эта классификация по существу очень близка к установленным древними индусами четырем кастам, а именно: шудры (рабочие), вайшьи (земледельцы, домовладетели, торговцы), кшатрии (военачальники, исполнительная власть, вожди), брахманы (духовенство, интеллигенция). В аналитическом, в частности, в геометрическом аспекте эти четыре категории мировоззрения как-то незаметно превратились в четыре мерности абстрактного геометрического пространства, а в физическом аспекте - в четыре типа силового взаимодействия (сильное, слабое, электромагнитное и гравитационное). Еще один долго замалчиваемый в нашей стране замечательный российский мыслитель Георгий Иванович Гурджиев, просуммировав все эти аспекты, определил четыре пути познания. А именно: первый путь факира (развития физического тела), второй - путь монаха (веры, развития религиозного чувства и религиозной жертвы), третий путь йогина (знания, развития ума), и, наконец, четвертый - путь сознательный. Этот путь требует работы по всем трем направлениям одновременно. Он требует прежде всего понимания, или "знания как" (в отличие от "знания о"). В настоящей работе рассмотрен математический, точнее геометрический аспект категорий мировоззрения, учитывая, что математика - это универсальный; не нуждающийся в переводе на другие язык, памятуя слова Артура Эддингтона о том, что "Идеал, к которому мы стремимся, заключается в объединении всех наших сведений о физическом мире в единую науку, положения которой могут быть выражены в терминах геометрических, или квазигеометрических концепций". В этом аспекте, начиная с глубокой древности и до настоящего времени, выполнено множество работ и исследований от вполне корректных до откровенно спекулятивных. Но все они по каким-то причинам дружно игнорируют необходимость исследования общего для всех выполненных построений изначального момента: "печки, от которой пляшут", а именно самого понятия "точка". Попытка прояснить этот вопрос представляет собой основное содержание настоящей работы. Традиционно классификацию пространств в геометрическом аспекте производят по следующей схеме: нульмерное -
точка, не имеющая измерения; И во всех этих вариантах, исключая нульмерный, как обязательный атрибут построения присутствует движение, т.е. в' определенном смысле насилие, искусственность построения. Есть и такие варианты, когда точке предлагают двигаться комбинированным способом, меняя направления на перпендикулярные, образуя своим следом прямоугольники с диагоналями, затем эти прямоугольники вращают произвольными способами, образуя разнообразные фигуры типа тороидов, ленты Мебиуса, сфер, дуплекссфер и т.п. И на базе таких построений создаются теоретические модели с очень далеко идущими следствиями, как правило, доступными только самому автору построения. Разумеется, таким образом исследователь формирует свое собственное мировоззрение, поскольку человеческому разуму в процессе познания присущи только модельные представления, и с этим как будто никто не спорит. Но все-таки модели, претендующие на общественное признание, должны и просто обязаны строится с учетом наблюдаемых явлений и практического опыта, но не с помощью искусственных приемов. А по поводу изложенного нельзя не задать безусловно самый существенный вопрос. Каким образом и кто реально может обеспечить движение нереальной точки (не имеющей измерения) да еще к тому же по самым произвольным траекториям? Конечно, только изощрений ум построителя. Но к реалиям это не имеет никакого отношения, поскольку несуществующая точка не может оставлять следов. Абсурдность таких построений хорошо иллюстрирует пример со знаменитой лентой Мебиуса. Никаким образом не может быть построена лента, не имеющая толщины. А при ее наличии лента: Мебиуса топологически превращается в обыкновенный тор, и все ее надуманные "замечательные" свойства исчезают "как дым". В конце концов, разве можно, допустимо ли так рассуждать: "Вот ты видишь и осязаешь толщину ленты, но, прошу тебя, считай, что ее нет!". Так можно очень далеко пойти. И таких примеров не счесть. Поскольку нет вразумительного ответа на поставленный вопрос, нет никакого смысла ставить остальные типа того, как обеспечить манипулирование следами точки, которые просто не могут образоваться? "Правила игры" достаточно строги. Если что-то критикуешь, изволь предложить альтернативу. Безусловно. Отправной момент альтернативы заключается в том, что точка не может быть "бестелесной", поскольку, согласно прекрасной мысли замечательного российского космиста Александра Леонидовича Чижевского "... в каждой точке Мир, весь Мир сосредоточен". (AJI. Чижевский, "К Гиппократу"). Достаточно наметить эту точку и хорошенько ее рассмотреть, не пытаясь гонять этот "весь Мир" по всевозможным направлениям. Сколь ни мала была бы выбранная точка, рассмотреть ее можно либо приблизившись, либо с помощью микроскопа, либо просто поставив корректный мысленный эксперимент. Например, сохраняя подобие, мысленно увеличить в несколько раз. Естественно предположить, что любая такая точка обладает объемом. А поскольку наиболее устойчивой формой объема служит сфероид, то и в качестве предмета исследования целесообразно выбрать именно сферический объем. Но предварительно следует обратить внимание на довольно-таки тонкий момент, как правило, оставляемый без внимания. Используя числовой метод анализа, необходимо помнить, что число представляет собой количественную меру, в любом случае характеризующую именно объем. Иными словами, понятия число и объем адекватны. И когда говорится, например, что длина такой-то линии составляет столько-то единиц, это значит, что объем этой линии именно таков, просто при этом ширина и толщина линии приняты за единичные значения, как бы "высветив" определяющий параметр. То же самое можно сказать и относительно числового значения, определяющего поверхность, когда за единицу оказывается принятой толщина. Проекция на плоскость увеличенного до удобных для исследования размеров точечного сфероида представляет собой круг, ограниченный окружностью радиуса R, рис. 1.
Памятуя о том, что точечный сфероид представляет собой нуль-пространство, при рассмотрении его в увеличенном масштабе оказывается возможным выделить, в нем одномерное пространство в виде окружности, либо любой другой линии на поверхности сфероида, двумерное пространство, представляющее собой поверхность сфероида и, наконец трехмерное пространство, представляющее собой объем сфероида. Фокус? Ничего подобного! Это просто геометрическая интерпретация того самого четвертого пути, о котором говорил Г.И. Гурджиев. Иными словами, при совместном рассмотрении три типа пространств (одномерное, двумерное и трехмерное) сливаются в четвертое - нульмерное. Нульмерность, или четвертая категория мировоззрения предопределяет целостное восприятие предмета, или явления, а не последовательное рассмотрение в тех, или иных аспектах. П.Д. Успенский так характеризует четвертую категорию: "Чувство четырехмерного пространства. Ощущение прошедшего и будущего как настоящего. Пространственное ощущение времени. Существование прошедшего и будущего вместе с настоящим и вместе одно с другим." Психологическая характеристика этой категории такова: "Интуиция. Непосредственное общение сознании. Непосредственное познание". Очень показательно сравнение характеристик, сформулированных П.Д. Успенским, для четвертой и первой категорий мировоззрения, которая представляет собой "Чувство одномерного пространства. Мир па линии. Линия как пространство. Все остальное как время. Все, кроме одной неподвижной линии, в движении". И мораль первой категории: "Бессознательные действия, (как действия спящего человека). Отсутствие морали". Это сравнение приведено здесь для того чтобы показать, в каком состоянии находится современная научная парадигма, узаконившая именно одномерный подход к изучению явлений путем создания всеобъемлющих систем физических единиц (Гауссовой, либо СИ), в которых в качестве основной пространственной единицы принята единица длины (сантиметр, либо метр), а остальные пространственные меры оказываются производными от меры длины (квадратные и кубические сантиметры и метры). И это предопределяет неспособность охватить явление в целом. Последствия хорошо известны. Так в аспекте общечеловеческой деятельности одномерность приводит к узкой специализации, по сути к умственной ограниченности. Исследование проекции точечного сфероида выявляет многие его замечательные свойства. Важно отметить, что необходимым условием существовать объекта является его пульсация. В противном случае исчезает граница между поверхностью объекта и окружающей средой. Только пульсирующий объект может быть обнаружен. А по отношению к сфероиду это предопределяет периодическое изменение его объема, а следовательно и радиуса окружности его плоской проекции. В свою очередь это пульсирующее состояние невозможно без наличия в центральной части сфероида некоторого образования (ядра), объем которого в положении, соответствующем наибольшему объему сфероида, равен приращению объема по сравнению с минимальным. На рис. 2 изображена проекция сфероида в положении наибольшего объема.
В/2 Рис. 2. Проекция сфероида (центральное сечение) в положении наибольшего объема. Трудно ответить па вопрос, а кто заставляет объекты пульсировать? Безусловно, это фундаментальный Закон Существования. И, если мы что-то видим, или выделяем, это обязательно пульсирует. В противном случае никакие наблюдения и построения просто невозможны. В зависимости от
величины приращения объема пульсирующего
сфероида могут возникнуть различные режимы
пульсации, а именно:
Рис. 3. Типы вибраторов. Как было отмечено, ядро сфероида (рис. 2) по своему объему равно приращению объема сфероида в процессе пульсации. Из этого следует, что величина поверхности ядра равна величине приращения поверхности сфероида, а длина окружности ядра в его сечении центральной плоскостью равна приращению длины окружности сфероида в том же сечении. Если в процессе пульсации сфероида приращение его центральной окружности составляет величину "В", то, естественно, приращение половины окружности равно величине D/2, рис. 2. Отношение хорды, стягивающей дугу В/2, к диаметру центрального круга сечения сфероида в аналитической форме может быть представлено как К = sin(B/4) .... (1) Поскольку величина отрезка (хорды), стягивающего дугу Д/2, представляет собой длину волны, характеризующей величину приращения дуга окружности сфероида в процессе пульсации, то по формуле (1) можно определить, или задать тип вибратора и соответственно установить режим пульсации. При К=1 В=360". В этом случае оказывается сформированным вибратор поглощения. Величина центрального ядра сфероида по всем параметрам равна самому сфероиду. В качестве характеристической константы этого режима можно принять соотношение объема ядра сфероида и его центрального ядра.
При К=1/2 8=120'. В этом случае оказывается сформированным вибратор поглощения-излучения. Объем центрального ядра сфероида составляет его 1/27 часть. Величина поверхности ядра в 9 раз меньше поверхности сфероида, а длина дуги окружности соответственно меньше в 3 раза. В качестве характеристической константы этого режима можно принять соотношение объемов сфероида и его ядра.
При К=1/4 В=-(57.9'1)'1. В этом случае оказывается сформированным вибратор излучения. Соотношение между объемом сфероида и объемом его ядра составляет 240.2401. Соотношение поверхностей 38.6453, соотношение дуг окружностей 6.2165. Характеристическая константа.
Последний из рассмотренных режимов можно определить в качестве критического, границы перехода в состояние чистого излучения, когда становится неизбежным процесс деструктуризации сфероида. И указанные числовые соотношения приобретают таким образом смысл фундаментальных величин, характеризующих трехмерное, двумерное и одномерное пространства. Эти результаты из разряда замечательных, поскольку они, полученные чисто умозрительно на основе элементарных вычислений, подтверждают и в ряде случаев уточняют результаты фундаментальных теоретических и практических исследований. А именно: - Аналитическая структура, экспериментально установленная для атомного ядра, полностью совпадает с рассмотренной структурой пульсирующего сфероида. В тоже время известно, что в естественных условиях последний устойчивый химический элемент, замыкающий ряд, - это уран-238, обладающий относительной массой (что эквивалентно относительному объему) 238. Иными словами, теоретический предел устойчивости, определяемый в числовом значении А=240.2401, убедительно подтверждается на практике существованием замыкающего ряд устойчивости химического элемента уран-238. Сама природа подтвердила эффективность рассматриваемого метода. - Число 6.2165... удивительно напоминает значение 271, теоретически определяемое как отношение длины окружности к ее радиусу. Однако, учитывая сказанное в начале настоящей работы о некорректности определения значений бестелесных геометрических построений, а тем более соотношений (между собой), приходится признать, что знаменитое число К не отражает реальное положение вещей. Иное дело в рассмотренном случае пульсирующего сфероида. Здесь толщина линии окружности четко проявлена крайними положениями поверхности сфероида в моменты его максимального и минимального значения объема. Учитывая отмеченное ранее, здесь длина окружности определена как объемная величина, что позволяет считать ее более пригодной для реальных расчетов. В силу изложенного, величина А=240.2401 приобретает статус универсальной мировой постоянной. Характеризуя критический объем, она автоматически включает в себя характеристики всех остальных типов пространств и взаимодействий. Более того, на этой основе оказалось возможным найти.
|