В данной статье изложен принцип, лежащий в основе алгоритма сжатия
PPH. Что же может заставить лезть в столь избитую тему, как хранение картинок? Прежде всего сложность, присущая распространенному алгоритму JPEG, кажущаяся мне совершенно неоправданной и пугающей.Все алгоритмы сжатия изображений в той или иной степени используют свойства этого множества информации. Здесь будет не лишним задуматься, какими же свойствами обладают картинки? Коротко можно сказать, что изменение яркости и цвета в большей части картинки происходит “медленно”, а цвет имеет свойство меняться совсем медленно. Итак имеем:
малое отличие друг от друга соседних элементов изображения
(1)Сначала рассмотрим случай с двумя элементами (соседями) и попробуем извлечь из этого выгоду.
Два числа.
Есть два числа А и Б, обладающие свойством (1), набор (А,Б) можно представить в виде (
s,d), где s = А + Б, d = Б - А . В результате имеем преобразование:(А
, Б) ® (s, d),новая пара (
s,d) хороша тем, что вследствие свойства (1) d является небольшой величиной, а значит для хранения этого числа требуется меньше единиц информации.Примечание: в случае с целыми числами, как у картинок,
s и d имеют одинаковую четность, следовательно, можно делить s на два (с округлением в одну сторону), при этом информация не потеряется, а мы будем иметь s в тех же пределах, что А и Б, и в паре с ним маленький d.В реальном изображении обычно присутствуют более чем два элемента (пиксела), а значит и более одной пары соседей.
Длинный случай
В случае с большим количеством элементов можно разбить их на пары (А,Б). Для простоты возьмем за количество элементов 2N.
В результате преобразования каждой пары (А,Б) получаем N пар (
s,d).
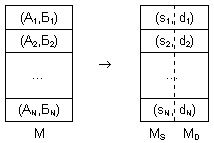
Теперь разделим пары (
s,d) на два множества MS и MD, как это показано на рисунке 1. Несложно заметить, что размер каждого из них равен N, а множество MD состоит из небольших по абсолютному значению величин.Длинный случай в рекурсии
Представленное преобразование множества M в пару (M
S,MD) можно углубить, т.е. применить преобразование M ® (MS,MD) к полученным множествам MS и MD.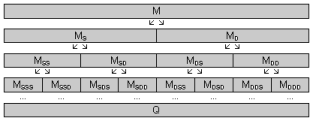
Сведем все в указанном на рисунке 2 порядке в множество Q. Если внимательно посмотреть на полученное множество, то внимание привлекает интересная особенность, а именно, что слева стоят большие по абсолютному значению элементы, а справа меньшие. Но это только на первый взгляд, на самом деле распределение задается характером множества M. Исследование показало, например, что множество M
SDDD… обычно имеет меньшие по абсолютному значению элементы, чем множество MDSSS….Можно сказать, что каждый элемент множества Q имеет свой уникальный смысл, являясь суммой всех элементов множества M с разным знаком. Однако, те из элементов Q, чье абсолютное значение больше, имеют более важное значение для восстановления
M, т.к. кроют в себе наиболее значимые особенности M. В то же время эксперимент показывает, что если обнулить те элементы Q что ниже (по абсолютному значению) некоторого порога p и затем восстановить M, то результат практически не отличается от исходного M при обнулении половины элементов Q.Количество вычислений в задаче рекурсивного преобразования
M в Q несложно показать. Сложность задачи разложения M на пару (MS,MD) прямо пропорциональна N - количеству элементов в M. А уровней разложения будет log2N, соответственно сложность полного преобразования эквивалентна Nlog2N.Двумерный случай
В случае с картинками мы имеем двумерную таблицу значений элементов изображения (пикселов), следовательно необходимо учесть оба измерения.
Возьмем упрощенный случай, когда изображение имеет размер 2nx2m и хранится в множестве M2. Тогда преобразуем M2 в M следующим образом:
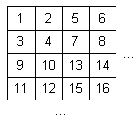
Данное преобразование замечательно тем, что каждая пара полученного множества
M (v1,v2),(v3,v4),(v5,v6)… получается из пары M2, состоящей из соседних элементов M2. Что примечательно, получаемые при преобразовании M ® Q множества MS, MD, MSS, MSD и т.д., обладают тем же свойством.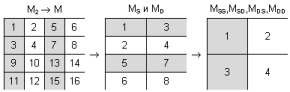
Преобразовав M
2 ® M ® Q, получаем набор коэффициентов Q, который необходимо сохранить.Сохранение множества Q с потерями
Как упоминалось ранее, значимость элементов Q для восстановления исходного изображения распределена не равномерно. А именно, важность элемента (относительно восстановления) эквивалентна его абсолютному значению.
Здесь можно пойти разными путями. Я могу показать свое решение.
Определим некоторое натуральное число
F как параметр точности, и преобразуем Q в Q’ так, что каждый элемент Q’ равен соответствующему элементу из Q деленному нацело на F. Как видно из этого преобразования, все элементы, абсолютное значение которых меньше F, обнулились, а остальные при восстановлении будут кратны F. При этом относительная точность (отношение первоначального к восстановленному) будет выше у изначально больших элементов.Полученное множество Q’ можно сохранять, как душа пожелает (тему можно развернуть
).Многомерный случай
Очевидно, что, при увеличении количества измерений, у элемента из Mn возрастает количество соседних элементов. Это приводит к тому, что полученное множество Q содержит меньшую долю значимых коэффициентов. А значит, и сохранять с потерями соответствующие множества можно эффективнее.
Автор полагает, что степень сжатия с приемлемыми потерями (отношение исходного количества информации к результату) для множества Mn равна w n, где w - показатель потери качества. Например, в случае с видео можно добиться лучшего коэффициента сжатия, если сжимать ряд кадров, как единое исходное множество.
Цвет
Как известно, информация о цвете употребляется глазом человека в гораздо меньших объемах, чем информация о яркости. Тем не менее компьютерное представление цветного изображения подразумевает утроение количества информации за счет разложения информации о цвете в три слоя (RGB). С этим необходимо бороться, тем более при сжатии картинок. Существует общепризнанная схема преобразования RGB-слоев в YCbCr-слои, призванная отделить слои, представляющие информацию о цвете от слоя яркости, следующим образом:
Cb = -0.1687R -0.3313G +0.5 B + 128 Cr = 0.5 R -0.4187G -0.0813B + 128 G = Y - 0.34414(Cb-128) – 0.71414 (Cr-128) B = Y + 1.772 (Cb-128) Заметьте, что
Примечание: в нашем случае, когда интервал получаемых значений не критичен, 128 можно смело заменить на 0.
Y = 0.299 R +0.587 G +0.114 B
R = Y + 1.402 (Cr-128)
Преобразование RGB ® YCbCr
Преобразование YCbCr ® RGB
При сжатии YCbCr-слоев достаточно сложных (в т.ч. и в смысле цвета) картинок автор нашел весьма любопытным факт, что при сжатии оба “цветовых” слоя (Cb и Cr) вместе требуют для приемлемого качества порядка 10-15% общего объема сжатого материала.
Эпилог
Хотелось бы отметить некоторую деталь: вычисления, основанные на алгоритме преобразования Mn ® M ® Q на 90% состоят из операций сложения и вычитания. Лишь сохранение Q с потерями требует работы с битами и, соответственно, съедает больше времени.
Автор, на основе вышеизложенного и оригинального метода сохранения множества Q, разработал алгоритм сжатия картинок, по качеству близкий (иногда опережающий) к известному алгоритму JPEG. Работу вместе с исходным текстом программ (на Delphi) можно посмотреть в интернете: http://popitch.narod.ru/pph/
Буду рад критическим замечаниям пришедшим по почте.
Картинка уже преобразована в один (в случае с черно-белым изображением) или три (Y, Cb, Cr – исходные слои) множества Q. Теперь их необходимо сохранить. Предлагаю описание метода, пришедшего в результате предпринятых изысканий. Предлагаемый алгоритм не претендует на идеальность.
Для начала введем параметр точности сохранения, пусть это будет натуральное число F, с точностью до которого будут сохранены все элементы множества Q. Отметим, что Q состоит из 2m+n коэффициентов, полученных преобразованием из двумерного множества M2 размером 2mx2n.
Преобразование Q à
QFКаждый элемент из Q делится на F и результат записывается в Q
F. Далее сохраняем полученные “сливки”.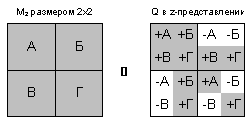
Рис. 1 Преобразование M
2 à QПримечание: здесь кроется маленькая хитрость. Обычно при делении числа нацело, результат округляется в сторону нуля, а значит восстановленные значения тоже будут ближе к нулю. Все, кроме первого (первый – M
SSS… является суммой M), коэффициенты из Q являются суммой всех членов M с разным знаком. Иначе говоря, разностью двух областей M2, а значит, округление в сторону нуля приведет к потери контрастности (станет ближе к нулю разность соседних элементов). Выход заключается в округлении (при делении) в ближайшую сторону, при котором контрастность практически в равной степени где-то повысится, а где-то уменьшится.Точное сохранение Q
FАлгоритм выглядит следующим образом:
1. p=1, pold=0, Nold = количество_элементов_в_QF
2. создадим массив битов B длиной в N
old бит, в который о всех из QF, что по абсолютному значению не меньше pold:вместе с тем подсчитаем количество установленных битов в переменную N
3. сохраним B (размером в Nold бит) с помощью специальной процедуры, см. ниже.
4. если N ¹ 0, то: Nold = N, pold = p, p = 2p, переходим к пункту 2.
Таким образом, сначала сохранится массив B, указывающий на ненулевые элементы QF. Далее – массив B рассказывающий о тех ненулевых, что по абсолютному значению не меньше 2. Потом о тех, кто по модулю не меньше 2, укажем кто еще и не меньше 4. 8, 16 и т.д.
Короче говоря, мы сохранили старшие биты абсолютных значений всех элементов QF.
5. сохраним для каждого элемента
QF: все биты его абсолютного значения, которые младше максимально сохраненного (без сжатия)6. для всех ненулевых элементов
QF: сохраним их знак (1 если больше 0, иначе 0), тоже без сжатия (просто в поток).Вот почти и все. Осталось только уяснить как сжимать массив битов
B. Укажу на этот раз лишь, что в начале массива всегда преобладают единицы, а в конце нули, и это надо обязательно использовать.Размер картинки
Мы почти научились сохранять множество
M2, но только размером 2mx2n. Сначала автор решил преобразовывать картинку из любого размера в 2mx2n, но при этом приходилось делать два преобразования (туда – обратно), что сжирало время и делало изображение нерезким. Значит ничего не поделаешь, а изображение придется резать на куски.Разрежем, для примера, число на составные части размером 2
x (рис. 2а.) и картинку (рис. 2б).а)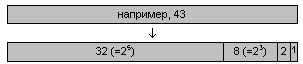
б)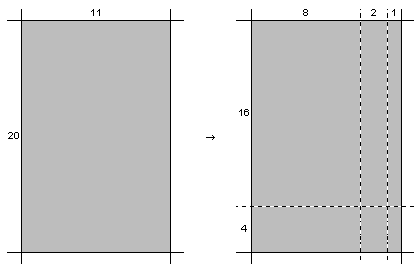
рис. 2 Почикать на кусочки: а – число, б – картинку.
Как видно из примера, получилось 6 частей требуемого размера. В худшем случае их может получиться многовато, а именно - 100 в случае с исходным размером картинки 1023
x1023, это не хорошо! Если читатель может придумать что-то лучше, прошу сообщить мне о находке.Еще прошу сообщить, если известно, где можно найти подробное описание всех процедур, применяемых в алгоритме
wavelet, некоторое сходство с коим было обнаружено внимательным читателем предыдущей главы.В следующей главе мы обсудим не влезшее в данное описание сжатие массива битов
B, основанное на его одном замечательном свойстве.
Пожалуй, самый процессоро-загружающий этап сжатия/восстановления. Итак, имеется массив бит B с преобладанием установленных элементов вначале и неустановленных в конце.
Перво-наперво, сохраним число установленных бит с учетом максимального значения, равного размеру массива. Далее вызываем процедуру, сохраняющую расположение установленных бит.
Процедура является рекурсивной и на входе получает: B – массив битов, N – размер массива, M – количество установленных бит. Из комбинаторики имеем: количество вариантов расстановки M бит в массиве B равно количеству сочетаний по M из N –
CMN.Пополам
Если это значение больше максимально допустимого в переменной типа Integer, то делим множество B пополам, подсчитываем M
1 – количество установленных бит в первой половине, сохраняем это количество (во второй половине становится тоже известно, потому как M1+M2=M), и вызываем сохранение обеих половин.Примечание: можно оптимизировать сохранение за счет того, что иногда M
1 находится на отрезке более узком, чем [0, SIZE/2], а именно интервал значений числа M1 равен [max(0,M-SIZE/2), min(M,SIZE/2)]. Значит сохранить остается только разность между M1 и минимальным значением отрезка с учетом, что максимальное значение этой разности равно длине того же отрезка.Код
В случае же, когда ограничения числа типа Integer не мешают нам поместить код комбинации в переменной, мы можем сохранить число, кодирующее данную комбинацию установленных бит. Например, если в массиве из 100 бит установленных всего 5 (или 95), то количество различных комбинаций равно 75287520, значит код комбинации займет 27 бит, т.к. 2
26<75287520<=227, налицо сжатие почти в 4 раза.Код комбинации вычисляется так. При установленном первом бите код равен коду подмножества
B состоящего из всех остальных битов (всего CM-1N-1 комбинаций), иначе сумме CM-1N-1 и кода того же подмножества, состоящего теперь из CMN-1 комбинаций, т.к. количество установленных бит не изменилось. Заметьте: CMN = CMN-1 + CM-1N-1. Алгоритм может показаться рекурсивным, но он легко реализуется циклом.Реализацию данного алгоритма на Delphi см.
http://popitch.narod.ru/pph/pphsource.zip.Схема
В целом алгоритм сжатия выглядит следующим образом:
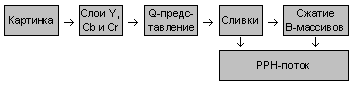
Вот теперь все! Вроде бы, надеюсь описывать алгорим восстановления нет необходимости, хотя…
Тут кто-то предложил музыкой заняться, ничего в ней не понимаю, посмотрим.
© Сережа Попов, 2001-02-20