
Данную главу нельзя рассматривать как учебник по языку Пролог, а только как краткий "ликбез", служащий для иллюстрации принципов продукционного программирования, описанных выше.
Объекты данных в Прологе называются термами. Терм может быть константой, переменной или составным термом (структурой). Константами являются целые и действительные числа, например:
0, -l, 123.4, 0.23E-5,
(некоторые реализации Пролога не поддерживают действительные числа).
К константам относятся также атомы, такие, как:
голди, а, атом, +, :, 'Фред Блогс', [].
Атом есть любая последовательность символов, заключенная в одинарные кавычки. Кавычки опускаются, если и без них атом можно отличить от символов, используемых для обозначения переменных. Приведем еще несколько примеров атомов:
abcd, фред, ':', Джо.
Полный синтаксис атомов описан ниже.
Как и в других языках программирования, константы обозначают конкретные элементарные объекты, а все другие типы данных в Прологе составлены из сочетаний констант и переменных.
Имена переменных начинаются с заглавных букв или с символа подчеркивания "_". Примеры переменных:
X, Переменная, _3, _переменная.
Если переменная используется только один раз, необязательно называть ее. Она может быть записана как анонимная переменная, состоящая из одного символа подчеркивания "_". Переменные, подобно атомам, являются элементарными объектами языка Пролог.
Завершает список синтаксических единиц сложный терм, или структура. Все, что не может быть отнесено к переменной или константе, называется сложным термом. Следовательно, сложный терм состоит из констант и переменных.
Теперь перейдем к более детальному описанию термов.
Константы известны всем программистам. В Прологе константа может быть атомом или числом.
Атом представляет собой произвольную последовательность символов, заключенную в одинарные кавычки. Одинарный символ кавычки, встречающийся внутри атома, записывается дважды. Когда атом выводится на печать, внешние символы кавычек обычно не печатаются. Существует несколько исключений, когда атомы необязательно записывать в кавычках. Вот эти исключения:
1) атом, состоящий только из чисел, букв и символа подчеркивания и начинающийся со строчной буквы;
2) атом, состоящий целиком из специальных символов. К специальным символам относятся:
+ - * / ^ = : ; ? @ $ &
Заметим, что атом, начинающийся с /*, будет воспринят как начало комментария, если он не заключен в одинарные кавычки.
Как правило, в программах на Прологе используются атомы без кавычек.
Атом, который необязательно заключать в кавычки, может быть записан и в кавычках. Запись с внешними кавычками и без них определяет один и тот же атом.
Внимание: допустимы случаи, когда атом не содержит ни одного символа (так называемый 'нулевой атом') или содержит непечатаемые символы. (В Прологе имеются предикаты для построения атомов, содержащих непечатаемые или управляющие символы.) При выводе таких атомов на печать могут возникнуть ошибки.
Большинство реализации Пролога поддерживают целые и действительные числа. Для того чтобы выяснить, каковы диапазоны и точность, чисел следует обратиться к руководству по конкретной реализации.
Понятие переменной в Прологе отличается от принятого во многих языках программирования. Переменная не рассматривается как выделенный участок памяти. Она служит для обозначения объекта, на который нельзя сослаться по имени. Переменную можно считать локальным именем для некоторого объекта.
Синтаксис переменной довольно прост. Она должна начинаться с прописной буквы или символа подчеркивания и содержать только символы букв, цифр и подчеркивания.
Переменная, состоящая только из символа подчеркивания, называется анонимной и используется в том случае, если имя переменной несущественно.
Областью действия переменной является утверждение. В пределах утверждения одно и то же имя принадлежит одной и той же переменной. Два утверждения могут использовать одно имя переменной совершенно различным образом. Правило определения области действия переменной справедливо также в случае рекурсии и в том случае, когда несколько утверждений имеют одну и ту же головную цель. Этот вопрос будет рассмотрен в далее.
Единственным исключением из правила определения области действия переменных является анонимная переменная, например, “_” в цели любит(Х,_). Каждая анонимная переменная есть отдельная сущность. Она применяется тогда, когда конкретное значение переменной несущественно для данного утверждения. Таким образом, каждая анонимная переменная четко отличается от всех других анонимных переменных в утверждении.
Переменные, отличные от анонимных, называются именованными, а неконкретизированные (переменные, которым не было присвоено значение) называются свободными.
Структура состоит из атома, называемого главным функтором, и последовательности термов, называемых компонентами структуры. Компоненты разделяются запятыми и заключаются в круглые скобки.
Приведем примеры структурированных термов:
собака(рекс), родитель(Х,У).
Число компонент в структуре называется арностью структуры. Так, в данном примере структура собака имеет арность 1 (записывается как собака/1), а структура родитель -арность 2 (родитель/2). Заметим, что атом можно рассматривать как структуру арности 0.
Для некоторых типов структур допустимо использование альтернативных форм синтаксиса. Это синтаксис операторов для структур арности 1 и 2, синтаксис списков для структур в форме списков и синтаксис строк для структур, являющихся списками кодов символов.
Структуры арности 1 и 2 могут быть записаны в операторной форме, если атом, используемый как главный функтор в структуре, объявить оператором (см. гл. 6).
В сущности, список есть не что иное, как некоторая структура арности 2. Данная структура становится интересной и чрезвычайно полезной в случае, когда вторая компонента тоже является списком. Вследствие важности таких структур в Прологе имеются специальные средства для записи списков. Возможности обработки списков рассматриваются в разд. 5.1.
Строка определяется как список кодов символов. Коды символов имеют особое значение в языках программирования. Они выступают как средство связи компьютера с внешним миром. В большинстве реализации Пролога существует специальный синтаксис для записи строк. Он подобен синтаксису атомов. Строкой является любая последовательность символов, которые могут быть напечатаны (кроме двойных кавычек), заключенная в двойные кавычки. Двойные кавычки в пределах строки записываются дважды “”.
В некоторых реализациях Пролога строки рассматриваются как определенный тип объектов подобно атомам или спискам. Для их обработки вводятся специальные встроенные предикаты. В других реализациях строки обрабатываются в точности так же, как списки, при этом используются встроенные предикаты для обработки списков. Поскольку все строки могут быть определены как атомы или как списки целых чисел, и понятие строки является чисто синтаксическим, мы не будем более к нему возвращаться.
Программа на Прологе есть совокупность утверждений. Утверждения состоят из целей и хранятся в базе данных Пролога. Таким образом, база данных Пролога может рассматриваться как программа на Прологе. В конце утверждения ставится точка “.”. Иногда утверждение называется предложением.
Основная операция Пролога - доказательство целей, входящих в утверждение.
Существуют два типа утверждений:
факт: это одиночная цель, которая, безусловно, истинна;
правило: состоит из одной головной цели и одной или более хвостовых целей, которые истинны при некоторых условиях.
Правило обычно имеет несколько хвостовых целей в форме конъюнкции целей.
Конъюнкцию можно рассматривать как логическую функцию И. Таким образом, правило согласовано, если согласованы все его хвостовые цели.
Примеры фактов:
собака(реке). родитель(голди.рекс).
Примеры правил:
собака (X) :- родитель (X.Y),собака (Y). человек(Х) :-мужчина(Х).
Разница между правилами и фактами чисто семантическая. Хотя для правил мы используем синтаксис операторов (более подробное рассмотрение операторного и процедурного синтаксисов выходит за рамки нашего курса), нет никакого синтаксического различия между правилом и фактом.
Так, правило
собака (X) :- родитель(Х,У),собака(У). может быть задано как
:-собака (X) ',' родитель(Х.У) .собака (Y).
Запись верна, поскольку :- является оператором “при условии, что”, а ',' - это оператор конъюнкции. Однако удобнее записывать это как
собака (X) :-родитель (X.Y),собака (Y).
и читать следующим образом: “ Х - собака при условии, что родителем Х является Y и Y - собака”.
Структуру иногда изображают в виде дерева, число ветвей которого равно арности структуры.

После записи утверждений в базу данных вычисления могут быть инициированы вводом запроса.
Запрос выглядит так же, как и целевое утверждение, образуется и обрабатывается по тем же правилам, но он не входит в базу данных (программу). В Прологе вычислительная часть программы и данные имеют одинаковый синтаксис. Программа обладает как декларативной, так и процедурной семантикой. Мы отложим обсуждение этого вопроса до последующих глав. Запрос обозначается в Прологе утверждением ?-, имеющим арность 1. Обычно запрос записывается в операторной форме: за знаком ?- следует ряд хвостовых целевых утверждений (чаще всего в виде конъюнкции).
Приведем примеры запросов:
?-собака(X). ?- родитель(Х.У),собака (Y).
или, иначе,
'?-'(собака(Х)) С?-') ','(родитель(Х„У”,собака (Y)).
Последняя запись неудобна тем, что разделитель аргументов в структуре совпадает с символом конъюнкции. Программисту нужно помнить о различных значениях символа ','.
Запрос иногда называют управляющей командой (директивой), так как он требует от Пролог-системы выполнения некоторых действий. Во многих реализациях Пролога для управляющей команды используется альтернативный символ, а символ ?- обозначает приглашение верхнего уровня интерпретатора Пролога. Альтернативным символом является :-. Таким образом,
:-write(co6aкa).
- это управляющая команда, в результате выполнения которой печатается атом собака. Управляющие команды будут рассмотрены ниже при описании ввода программ.
Введение списка утверждений в Пролог-систему осуществляется с помощью встроенного предиката consult. Аргументом предиката consult является атом, который обычно интерпретируется системой как имя файла, содержащего текст программы на Прологе. Файл открывается, и его содержимое записывается в базу данных. Если в файле встречаются управляющие команды, они сразу же выполняются. Возможен случай, когда файл не содержит ничего, кроме управляющих команд для загрузки других файлов. Для ввода утверждений с терминала в большинстве реализации Пролога имеется специальный атом, обычно user. С его помощью утверждения записываются в базу данных, а управляющие команды выполняются немедленно.
Помимо предиката consult, в Прологе существует предикат reconsult. Он работает аналогичным образом. Но перед добавлением утверждений к базе данных из нее автоматически удаляются те утверждения, головные цели которых сопоставимы с целями, содержащимися в файле перезагрузки. Такой механизм позволяет вводить изменения в базу данных. В Прологе имеются и другие методы добавления и удаления утверждений из базы данных. Некоторые реализации языка поддерживают модульную структуру, позволяющую разрабатывать модульные программы.
В заключение раздела дадим формальное определение синтаксиса Пролога, используя форму записи Бэкуса-Наура, иногда называемую бэкусовской нормальной формой (БНФ).
запрос ::- голова утверждения
правило ::– голова утверждения :- хвост утверждения
факт ::- голова утверждения
голова утверждения ::-атом | структура
хвост утверждения ::- атом структура,
термы ::-терм [,термы]
терм ::- число | переменная | атом | структура
структура ::-атом (термы)
Данное определение синтаксиса не включает операторную, списковую и строковую формы записи. Полное определение дано в приложении А. Однако, любая программа на Прологе может быть написана с использованием вышеприведенного синтаксиса. Специальные формы только упрощают понимание программы. Как мы видим, синтаксис Пролога не требует пространного объяснения. Но для написания хороших программ необходимо глубокое понимание языка.
Одним из наиболее важных аспектов программирования на Прологе являются понятия унификации (отождествления) и конкретизации переменных.
Пролог пытается отождествить термы при доказательстве, или согласовании, целевого утверждения. Например, в программе из гл. 1 для согласования запроса ?- собака(Х) целевое утверждение собака (X) было отождествлено с фактом собака (реке), в результате чего переменная Х стала конкретизированной: Х= рекc.
Переменные, входящие в утверждения, отождествляются особым образом - сопоставляются. Факт доказывается для всех значений переменной (переменных). Правило доказывается для всех значений переменных в головном целевом утверждении при условии, что хвостовые целевые утверждения доказаны. Предполагается, что переменные в фактах и головных целевых утверждениях связаны квантором всеобщности. Переменные принимают конкретные значения на время доказательства целевого утверждения.
В том случае, когда переменные содержатся только в хвостовых целевых утверждениях, правило считается доказанным, если хвостовое целевое утверждение истинно для одного или более значений переменных. Переменные, содержащиеся только в хвостовых целевых утверждениях, связаны квантором существования. Таким образом, они принимают конкретные значения на то время, когда целевое утверждение, в котором переменные были согласованы, остается доказанным.
Терм Х сопоставляется с термом Y по следующим правилам. Если Х и Y - константы, то они сопоставимы, только если они одинаковы. Если Х является константой или структурой, а Y - неконкретизированной переменной, то Х и Y сопоставимы и Y принимает значение Х (и наоборот). Если Х и Y - структуры, то они сопоставимы тогда и только тогда, когда у них одни и те же главный функтор и арность и каждая из их соответствующих компонент сопоставима. Если Х и Y - неконкретизированные (свободные) переменные, то они сопоставимы, в этом случае говорят, что они сцеплены. В (Таблица 2) приведены примеры отождествимых и неотождествимых термов.
Таблица 2. Иллюстрация унификации.
Терм1 | Терм2 | Отождествимы ? |
джек(Х) джек (личность) джек(Х,Х) джек(Х.Х) джек( . ) f(Y,Z) Х | джек (человек) джек (человек) джек(23,23) джек (12,23) джек(12,23) Х Z | да: Х=человек нет да: Х=23 нет да да: X=f(Y,Z) да: X=Z |
Заметим, что Пролог находит наиболее общий унификатор термов. В последнем примере (рис.2.1) существует бесконечное число унификаторов:
X-1, Z-2; X-2, Z-2; ....
но Пролог находит наиболее общий: Х=Z.
Следует сказать, что в большинстве реализации Пролога для повышения эффективности его работы допускается существование циклических унификаторов. Например, попытка отождествить термы f(X) и Х приведет к циклическому унификатору X=f(X), который определяет бесконечный терм f(f(f(f(f(...))))). В программе это иногда вызывает бесконечный цикл.
Возможность отождествления двух термов проверяется с помощью оператора =.
Ответом на запрос
?- 3+2=5.
будет
нет
так как термы не отождествимы (оператор не вычисляет значения своих аргументов), но попытка доказать
?-строка(поз(Х)) -строка(поз(23)).
закончится успехом при
Х=23.
Унификация часто используется для доступа к подкомпонентам термов. Так, в вышеприведенном примере Х конкретизируется первой компонентой терма поз(23), который в свою очередь является компонентой терма строка.
Бывают случаи, когда надо проверить, идентичны ли два терма. Выполнение оператора = = заканчивается успехом, если его аргументы - идентичные термы. Следовательно, запрос
?-строка(поз(Х)) --строка (поз (23)).
дает ответ
нет
поскольку подтерм Х в левой части (X - свободная переменная) не идентичен подтерму 23 в правой части, Однако запрос
?- строка (поз (23)) --строка (поз (23)).
дает ответ
да
Отрицания операторов = и - = записываются как \= и \= = соответственно.
В этой главе показано, каким образом Пролог выполняет арифметические операции. Будут описаны арифметические операторы и их использование в выражениях, а также рассмотрены встроенные предикаты, служащие для вычисления и сравнения арифметических выражений.
Язык Пролог не предназначен для программирования задач с большим количеством арифметических операций. Для этого используются процедурные языки программирования. Однако в любую Пролог-систему включаются все обычные арифметические операторы:
+ сложение
— вычитание
* умножение
/ деление
mod остаток от деления целых чисел
div целочисленное деление
В некоторых реализациях языка Пролог присутствует более широкий набор встроенных арифметических операторов.
Пролог позволяет также сравнивать арифметические выражения, используя следующие встроенные предикаты:
Диапазоны чисел, входящих в арифметические выражения, зависят от реализации Пролога. Например, система ICLPROLOG оперирует с целыми числами со знаком в диапазоне
–8388606 ... 8388607
Арифметическое выражение является числом или структурой. В структуру может входить одна или более компонент, таких, как числа, арифметические операторы, арифметические списковые выражения, переменная, конкретизированная арифметическим выражением, унарные функторы, функторы преобразования и арифметические функторы.
Числа. Числа и их диапазоны определяются в конкретной реализации Пролога.
Арифметические операторы. + - * / mod div
Арифметические списковые выражения. Если Х - арифметическое выражение, то список [X ] также является арифметическим выражением, например [1,2,3]. Первый элемент списка используется как операнд в выражении. Скажем,
X is ([l,2,3]+5)
имеет значение 6.
Арифметические списковые выражения полезны и при обработке символов, поскольку последние могут рассматриваться как небольшие целые числа. Например, символ "а" эквивалентен [97 ] и, будучи использован в выражении, вычисляется как 97. Поэтому значение выражения “р”+"А"-"а" равно 80, что соответствует коду ASCII для “Р”.
Переменная, конкретизированная арифметическим выражением. Примеры:
Х-5+2 и У-3*(2+А)
Унарные функторы. Примеры:
+(Х) и -(У)
Функторы преобразования. В некоторых реализациях Пролога имеется арифметика с плавающей точкой, а следовательно, и функторы преобразования. Например:
float (X) преобразует целое число Х в число с плавающей точкой.
Математические функторы. Пример: квадрат(Х) объявлен как оператор и эквивалентен арифметическому выражению (Х*Х).
Атомы +, -, *, /, mod и div - обычные атомы Пролога и могут использоваться почти в любом контексте. Указанные атомы - не встроенные предикаты, а функторы, имеющие силу только в пределах арифметических выражений. Они определены как инфиксные операторы. Эти атомы являются главными функторами в структуре, а сама структура может принимать только описанные выше формы.
Позиция, приоритет и ассоциативность арифметических операторов четко заданы и перечислены в таблице операторов в гл. 6.
Арифметический оператор выполняется следующим образом. Во-первых, вычисляются арифметические выражения по обе стороны оператора. Во-вторых, над результатом вычислений выполняется нужная операция.
Арифметические операторы определяются Пролог-системой. Если мы напишем предикат
среднее (X,Y,Z) :- Z is (X+Y)/2.
то хотя можно определить среднее как оператор
?- ор(250^х, среднее).
но Пролог выдаст сообщение об ошибке, если встретит выражение Z is X среднее Y.
Это произойдет потому, что Х среднее Y не образует арифметического выражения, а среднее не является арифметическим оператором, определенным в системе.
Вычисление арифметических выражений
В Прологе не допускаются присваивания вида Сумма=2+4.
Выражение такого типа вычисляется только с помощью системного предиката is, например:
Сумма is 2 + 4.
Предикат is определен как инфиксный оператор. Его левый аргумент - или число, или неконкретизированная переменная, а правый аргумент - арифметическое выражение.
Попытка доказательства целевого утверждения Х is Y заканчивается успехом в одном из следующих случаев:
а) Х - неконкретизированная переменная, а результат вычисления выражения Y есть число;
б) Х - число, которое равно результату вычисления выражения Y. Цель Х is Y не имеет побочных эффектов и не может быть согласована вновь. Если Х не является неконкретизированной переменной или числом, или если Y - не арифметическое выражение, возникает ошибка.
Примеры:
D is 10- 5 заканчивается успехом и D становится равным 5
4 is 2 * 4 - 4 заканчивается успехом
2 * 4 - 4 is 4 заканчивается неудачей
a is 3 + 3 заканчивается неудачей
X is 4 + а заканчивается неудачей
2 is 4 - X заканчивается неудачей
Обратите внимание, что предикат is требует, чтобы его первый аргумент был числом или неконкретизированной переменной. Поэтому М - 2 is 3 записано неверно. Предикат is не является встроенным решателем уравнений.
Сравнение результатов арифметических выражений
Системные предикаты =:=, =\=, >, <, >= и <= определены как инфиксные операторы и применяются для сравнения результатов двух арифметических выражений.
Для предиката @ доказательство целевого утверждения X@Y заканчивается успехом, если результаты вычисления арифметических выражений Х и Y находятся в таком отношении друг к другу, которое задается предикатом @.
Такое целевое утверждение не имеет побочных эффектов и не может быть согласовано вновь. Если Х или Y - не арифметические выражения, возникает ошибка.
С помощью предикатов описываются следующие отношения:
Х =:= Y Х равно Y
Х =\= Y Х не равно Y
Х < Y Х меньше Y
Х > Y Х больше Y
Х <= Y Х меньше или равно Y
Х >= Y Х больше или равно Y
Использование предикатов иллюстрируют такие примеры:
а > 5 заканчивается неудачей
5+2+7 > 5+2 заканчивается успехом
3+2 =:= 5 заканчивается успехом
3+2 < 5 заканчивается неудачей
2 + 1 =\= 1 заканчивается успехом
N > 3 заканчивается успехом, если N больше 3, и неудачей в противном случае
Термы Пролога позволяют выразить самую разнообразную информацию. В настоящей главе мы рассмотрим два вида широко используемых структур данных: списки и бинарные деревья, и покажем, как они представляются термами Пролога.
СПИСКОВАЯ ФОРМА ЗАПИСИ
Задачи, связанные с обработкой списков, на практике встречаются очень часто. Скажем, нам понадобилось составить список студентов, находящихся в аудитории. С помощью Пролога мы можем определить список как последовательность термов, заключенных в скобки. Приведем примеры правильно построенных списков Пролога:
[джек, джон, фред, джилл, джон]
[имя (джон, смит), возраст (джек, 24), X]
[Х.У.дата (12,январь, 1986) ,Х]
[]
Запись [H|T] определяет список, полученный добавлением Н в начало списка Т. Говорят, что Н - голова, а Т - хвост списка [HIT]. На вопрос
?-L=[a | [b, c, d]]. будет получен ответ
L=[a, b, c, d]
а на запрос
?-L= [a, b, c, d], L2=[2 | L]. - ответ
L=[a, b, c, d], L2- [2, a, b, c, d]
Запись [Н | Т] используется для того, чтобы определить голову и хвост списка. Так, запрос
?- [X | Y]=[a, b, c]. дает
Х=а, Y=[b, c]
Заметим, что употребление имен переменных Н и Т необязательно. Кроме записи вида [H|T], для выборки термов используются переменные. Запрос
?-[a, X, Y]=[a, b, c].
определит значения
X=b
Y=c
а запрос
?- [личность(Х) | Т]=[личность(джон), а, b].
значения
Х=джон
Т=[а, Ь]
НЕКОТОРЫЕ СТАНДАРТНЫЕ ЦЕЛЕВЫЕ УТВЕРЖДЕНИЯ ДЛЯ ОБРАБОТКИ СПИСКОВ
Покажем на примерах, как можно использовать запись вида [Н | T] вместе с рекурсией для определения некоторых полезных целевых утверждений для работы со списками,
Принадлежность списку. Сформулируем задачу проверки принадлежности данного терма списку.
Граничное условие:
Терм R содержится в списке [H|T], если R=H.
Рекурсивное условие:
Терм R содержится в списке [H|T], если R содержится в списке Т.
Первый вариант записи определения на Прологе имеет вид:
содержится (R, L) :-
L=[H I T],
H=R.
содержится(Р, L) :-
L=[H|T],
содержится (R, T).
Цель L=[H I T] в теле обоих утверждений служит для того, чтобы разделить список L на голову и хвост.
Можно улучшить программу, если учесть тот факт, что Пролог сначала сопоставляет с целью голову утверждения, а затем пытается согласовать его тело. Новая процедура, которую мы назовем принадлежит, определяется таким образом:
принадлежит (R, [R | Т]).
принадлежит (R, [H | Т]) :- принадлежит (R, T).
На запрос
?- принадлежит(а, [а, Ь, с]).
будет получен ответ
да
на запрос
?- принадлежит(b, [a, b, с]).
- ответ
да
но на запрос
?- принадлежит(d, (a, b, c)).
Пролог дает ответ
нет
В большинстве реализации Пролога предикат принадлежит является встроенным.
Соединение двух списков. Задача присоединения списка Q к списку Р, в результате чего получается список R, формулируется следующим образом:
Граничное условие:
Присоединение списка Q к [] дает Q.
Рекурсивное условие:
Присоединение списка Q к концу списка Р выполняется так: Q присоединяется к хвосту Р, а затем спереди добавляется голова Р.
Определение можно непосредственно написать на Прологе:
соединить([],0,0).
соединить(Р,Q,Р) :-
Р=[НР | ТР],
соединить(TP, Q, TR),
R=[HP | TR].
Однако, как и в предыдущем примере, воспользуемся тем, что Пролог сопоставляет с целью голову утверждения, прежде чем пытаться согласовать тело:
присоединить([] ,Q,Q).
присоединить(HP | TP], Q, [HP | TR]) :-
присоединить (TP, Q, TR).
На запрос
?- присоединить [а, b, с], [d, e], L).
будет получен ответ
L = [a, b, c, d].
но на запрос
?- присоединить([a, b], [c, d], [e, f]).
ответом будет
нет
Часто процедура присоединить используется для получения списков, находящихся слева и справа от данного элемента:
присоединить (L [джим, р], [джек,.билл, джим, тим, джим, боб] ) .
L = [джек, билл]
R = [тим, джим, боб]
другие решения (да/нет)? да
L=[джек, билл, джим, тим]
R=[боб]
другие решения (да/нет)? да
других решений нет
Индексирование списка. Задача получения N-ro терма в списке определяется следующим образом:
Граничное условие:
Первый терм в списке [Н | Т] есть Н.
Рекурсивное условие:
N-й терм в списке [Н | Т] является (N-I)-м термом в списке Т.
Данному определению соответствует программа:
/* Граничное условие:
получить ([H | Т], 1, Н). /* Рекурсивное условие:
получить([Н | Т], N, У) :-
М is N - 1,
получить (Т, М ,Y).
Построение списков из фактов. Иногда бывает полезно представить в виде списка информацию, содержащуюся в известных фактах. В большинстве реализации Пролога есть необходимые для этого предикаты:
bagof(X,Y,L) определяет список термов L, конкретизирующих переменную Х как аргумент предиката Y, которые делают истинным предикат Y
setof(X,Y,L) все сказанное о предикате bagof относится и к setof, за исключением того, что список L отсортирован и из него удалены все повторения.
Если имеются факты:
собака(рекс).
собака (голди).
собака (фидо).
собака(реке).
то на запрос
?- bagof(D, co6aкa(D), L),
будет получен ответ
L=[реке, голди, фидо, рекс]
в то время как
?-setof(D, co6aкa(D), L). дает значение
L=[фидо, голди, рекc]
Пример: сложение многочленов
Теперь мы достаточно подготовлены к тому, чтобы использовать списки для решения задач. Вопрос, которым мы займемся, - представление и сложение многочленов.
Представление многочленов. Посмотрим, как можно представить многочлен вида
Р(х)=3+3х-4х^3+2х^9
Q(х)=4х+х^2-3х^3+7х^4+8х^5
Заметим, что каждое подвыражение (такое, как Зх ^3, Зх, 3) имеет самое большее две переменные компоненты: число, стоящее перед х, называемое коэффициентом, и число, стоящее после ^ - степень. Следовательно, подвыражение представляется термом
х(Коэффициент, Степень)
Так, 5х^2 записывается как х(5,2), х^З представляется как х(1,3), а поскольку х^0 равно 1, подвыражению 5 соответствует терм х(5,0).
Теперь запишем многочлен в виде списка. Приведенный выше многочлен Р(х), например, будет выглядеть следующим образом:
[x(3, 0), '+', x(3, l), '-', x(4, 3), '+', x(2, 9)]
Воспользуемся тем, что многочлен
3 + 3х - 4х^3 + 2х^9
допускает замену на эквивалентный
3 + 3х + (-4)х^3 + 2х^9 Тогда он выражается списком:
[х(3, 0), '+', х(3, 1), '+', х(-4, 3), '+', х(2, 9)]
В такой записи между термами всегда стоят знаки '+'. Следовательно, их можно опустить, и многочлен принимает окончательный вид:
[х(3, 0), х(3, 1), х(-4, 3), х(2, 9)]
Подразумевается, что между всеми термами списка стоят знаки '+'. Представлением многочлена Q(x) будет
[х(4, 1), х(1, 2), х(-3, 3), х(7, 4), х(8, 5)]
Сложение многочленов. Теперь напишем целевые утверждения для сложения двух многочленов. Сложение многочленов
3-2х^2+4х^3+6х^6
-1+3х^2-4х^3
в результате дает
2+х^2+6х^6
Аргументами целевого утверждения являются многочлены, представленные в виде списков. Ответ будет получен также в виде списка.
Сложение многочлена Р с многочленом Q осуществляется следующим образом:
Граничное условие:
Р, складываемый с [], дает Р.
[], складываемый с Q, дает Q.
Рекурсивное условие:
При сложении Р с Q, в результате чего получается многочлен R, возможны 4 случая:
а) степень первого терма в Р меньше, чем степень первого терма в Q. В этом случае первый терм многочлена Р образует первый терм в R, а хвост R получается при прибавлении хвоста Р к Q. Например, если Р и Q имеют вид
Р(х)=3х^2+5х^3
Q(x)=4x^3+3x^4
то первый терм R(x) равен 3х^2 (первому терму в Р(х)). Хвост R(x) равен 9х^3+3х^4, т.е. результату сложения Q(x) и хвоста Р(х);
б) степень первого терма в Р больше степени первого терма в Q. В данном случае первый терм в Q образует первый терм в R, а хвост R получается при прибавлении Р к хвосту Q. Например, если
Р(х)=2х^3+5х^'4
Q(x)=3x^3-x^4
то первый терм R(x) равен 3х^2 (первому терму в Q(x)), а хвост R(x) равен 2х^3+4х^4 (результату сложения Р(х) и хвоста Q(x));
в) степени первых термов в Р и Q равны, а сумма их коэффициентов отлична от нуля. В таком случае первый терм в R имеет коэффициент, равный сумме коэффициентов первых термов в Р и Q. Степень первого терма в R равна степени первого терма в Р (или Q). Хвост R получается при сложении хвоста Р и хвоста Q. Например, если Р и Q имеют вид
Р(х)=2х+3х^3
Q(x)=3x+4x^4
то первый терм многочлена R (х) равен 5х (результату сложения первого терма в Р(х) с первым термом в Q(x)). Хвост R(x) равен 3х^3+4х^4 (результату сложения хвоста Р(х) и хвоста Q(x));
г) степени первых термов в Р и Q одинаковы, но сумма коэффициентов равна нулю. В данном случае многочлен R равен результату сложения хвоста Р с хвостом Q. Например, если
р(х)=2+2х
Q(x)=2-3x^2
то
R(x)=2x-3x^2
(это результат сложения хвостов многочленов Р (х) и Q (х)).
Рассмотренный процесс сложения многочленов можно непосредственно записать на языке Пролог:
/* Граничные условия
слож_мн([], Q Q).
слож_мн(P, [], P).
/* Рекурсивное условие
/* (a)
слож_мн([x(Pc, Pp)|Pt], [x(Qc, Qp)|Qt],
[x(Pc,Pp)IRt]) :-
PpQp,
слож_мн(Рt, [х(Qс,Qр) | Qt], Rt).
/*(б)
слож_мн([x(Pc, Pp) | Pt], [x(Qc, Qp) | Qt],
[x(Qc, Qp) | Rt]) :-
PpQp,
слож_мн([x(Pc, Pp) | Pt], Qt, Rt).
/*(в)
слож_мн([x(Pc, Pp) | Pt], [х(Qc,Pp) | Qt],
[x(Rc, Pp) | Rt]) :-
Rc is Pc+Qc,
Rc =\= 0,
слож_мн(Pt, Qt,Rt).
/*(r)
слож_мн([х(Рс, Рр) | Pt],
[x(Qc.Pp) | Qt], Rt) :-
Re is Pc+Qc,
Rc =:= 0,
слож_мн(Pt, Qt, Rt).
Заметим, что в двух последних утверждениях проверка на равенство осуществляется следующим образом: степени первых термов складываемых утверждений обозначает одна и та же переменная Pp.
Списки как термы. В начале главы мы упомянули о том, что список представляется с помощью терма. Такой терм имеет функтор '.', Два аргумента и определяется рекурсивно. Первый аргумент является головой списка, а второй - термом, обозначающим хвост списка. Пустой список обозначается []. Тогда список [а, b] эквивалентен терму.(а,.(b, [])).
Таким образом, из списков, как и из термов, можно создавать вложенные структуры. Поэтому выражение
[[a, b], [c, d], [a], a]
есть правильно записанный список, и на запрос
?- [Н | Т]=[[а, b], с].
Пролог дает ответ
Н=[а, b]
Т=[с]
ПРЕДСТАВЛЕНИЕ БИНАРНЫХ ДЕРЕВЬЕВ
Бинарное дерево определяется рекурсивно как имеющее левое поддерево, корень и правое поддерево. Левое и правое поддеревья сами являются бинарными деревьями. На Рис. 2 показан пример бинарного дерева.
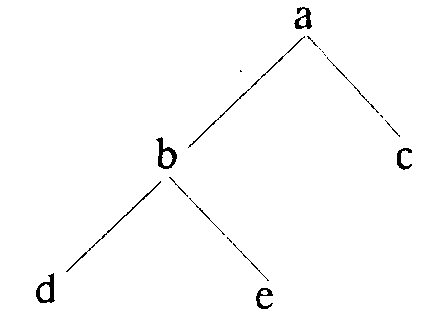
Рис. 2. Бинарное дерево.
Такие деревья можно представить термами вида
бд(Лд, К, Пд),
где Лд - левое поддерево, К - корень, а Пд - правое поддерево. Дл” обозначения пустого бинарного дерева будем использовать атом nil. Бинарное дерево на рис.5.2.1 имеет левое поддерево
бд(бд(nil, d, nil), b, бд(nil, е, nil))
правое поддерево
бд(nil,с, nil)
и записывается целиком как
бд(бд(бд(nil,d, nil), b, бд(nil,е, nil)), а, бд(nil, с, nil)).
ПРЕДСТАВЛЕНИЕ МНОЖЕСТВ С ПОМОЩЬЮ БИНАРНЫХ ДЕРЕВЬЕВ
Описание множеств в виде списков позволяет использовать для множеств целевое утверждение принадлежит, определенное ранее для списков.
Однако для множеств, состоящих из большого числа элементов, списковые целевые утверждения становятся неэффективными. Рассмотрим, например, как целевое утверждение принадлежит (см. предыдущий разд.) позволяет моделировать принадлежность множеству. Пусть L - список, описывающий множество из первых 1024 натуральных чисел. Тогда при ответе на запрос
?- принадлежит(3000, b).
Прологу придется проверить все 1024 числа, прежде чем заключить, что такого числа нет:
нет
Представление множества бинарным деревом позволяет добиться лучшего результата. При этом бинарное дерево должно быть упорядочено таким образом, чтобы любой элемент в левом поддереве был меньше, чем значение корня, а любой элемент в правом поддереве — больше. Поскольку мы определили поддерево как бинарное дерево, такое упорядочение применяется по всем поддеревьям. На Рис. 3 приведен пример упорядоченного бинарного дерева.
Дерево на Рис. 2 является неупорядоченным.
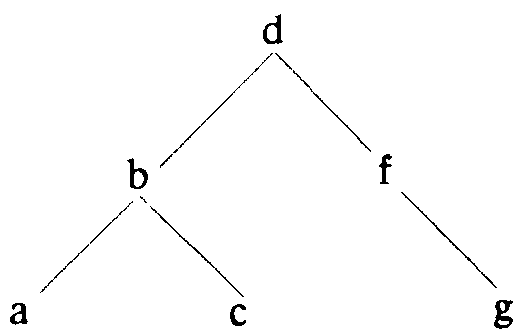
Рис. 3. Упорядоченное бинарное дерево.
Обратите внимание, что упорядочение приводит не к единственному варианту представления множества с помощью дерева. Например, на Рис. 4 изображено то же множество, что и на Рис. 3.
Будем называть линейным представление такого вида, как на Рис. 4, и сбалансированным - такое, как на Рис. 3.
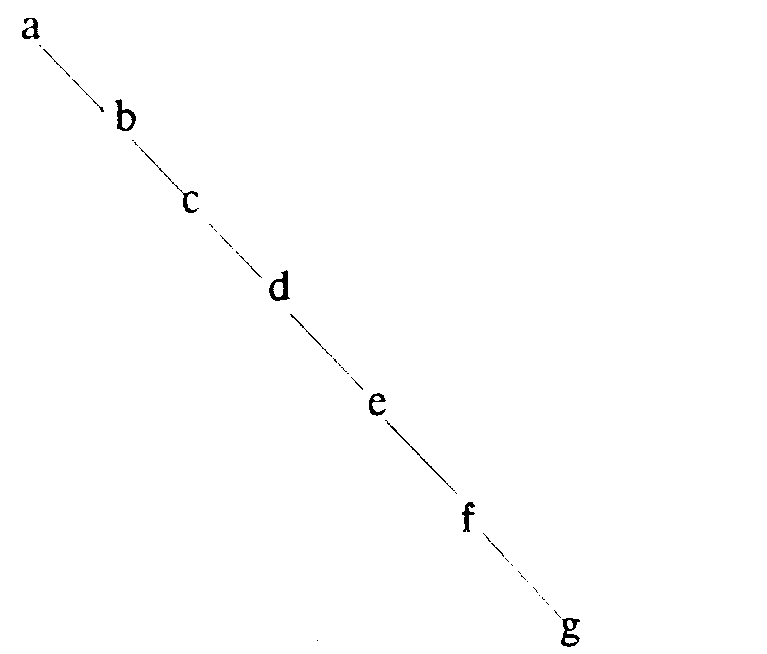
Рис. 4. Линейное представление.
Моделирование принадлежности множеству. Имея множество, описанное бинарным деревом, мы можем моделировать принадлежность множеству с помощью целевого утверждения принадлежит_дереву. При этом используется оператор @<, выражающий отношение “меньше, чем”, и оператор @>, выражающий отношение “больше, чем”.
/* Граничное условие: Х принадлежит
/* дереву, если Х является корнем.
принадлежит_дереву(Х, бд(Лд, Х, Пд)),
/* Рекурсивные условия
/* Х принадлежит дереву, если Х больше
/* значении корня и находится в правом
/* поддереве:
принадлсжит_дереву(Х, бд(Лд, У, Пд)) :- X@Y,
припадлежит_дереву(Х, Пд).
/* Х принадлежит дереву, если Х меньше
/* значения корня и находится в левом
/* поддереве:
принадлежит_дереву(Х, бд(Лд ,У ,Пд)) :-X@Y,
принадлежит_дереву(Х, Лд).
Если множество из первых 1024 чисел описать с помощью сбалансированного бинарного дерева Т, то при ответе на запрос
?- принадлежит_дереву(3000, Т).
Пролог сравнит число 3000 не более чем с 11 элементами множества. прежде чем ответит:
нет
Конечно, если Т имеет линейное представление, то потребуется сравнение 3000 с 1024 элементами множества.
Построение бинарного дерева. Задача создания упорядоченного бинарного дерева при добавлении элемента Х к другому упорядоченному бинарному дереву формулируется следующим образом:
Граничное условие:
Добавление Х к nil дает бд(nil, Х, nil).
Рекурсивные условия:
При добавлении Х к бд(Лд, К, Пд) нужно рассмотреть два случая, чтобы быть уверенным, что результирующее дерево будет упорядоченным.
1. Х меньше,чем К. В этом случае нужно добавить Х к Лд, чтобы получить левое поддерево. Правое поддерево равно Пд, а значение корня результирующего дерева равно К.
2. Х больше, чем К. В таком случае нужно добавить Х к Пд, чтобы получить правое поддерево. Левое поддерево равно Лд, а значение корня - К.
Такой формулировке задачи соответствует программа:
/* Граничное условие:
включ_бд(nil, Х, бд(nil, Х, nil)).
/* Рекурсивные условия:
/*(1)
включ_бд(бд(Лд, К, Пд), Х, бд(Лднов, К, Пд)) :-
Х@К,
включ_бд(Лд,Х,Лднов).
/*(2)
включ_бд(бд(Лд, К, Пд), Х, бд(Лд, К, Пднов)) :-
Х@К,
включ_бд(Пд, Х, Пднов).
На запрос
?- включ_бд(nil, d, Т1), включ_бд(Т1, а, Т2).
будут получены значения
Т1=бд(nil, d, nil)
Т2=бд(бд(nil, а, nil), d, nil)
Процедуру включ_бд() можно использовать для построения упорядоченного дерева из списка:
/* Граничное условие:
список_в_дерево([], nil).
/* Рекурсивное условие:
список_в_дерево([Н | Т], Бд) :-
список_в_дерево(Т, Бд2),
включ_бд(Н, Бд2, Бд).
Заметим, что включ_бд не обеспечивает построения сбалансированного дерева. Однако существуют алгоритмы, гарантирующие такое построение.
Механизм возврата и процедурная семантика
При согласовании целевого утверждения в Прологе используется метод, известный под названием механизма возврата. В этой главе мы показываем, в каких случаях применяется механизм возврата, как он работает и как им пользоваться. Описывается декларативная и процедурная семантика процедур Пролога. Завершается глава обсуждением вопросов эффективности.
При попытке согласования целевого утверждения Пролог выбирает первое из тех утверждений, голова которых сопоставима с целевым утверждением. Если удастся согласовать тело утверждения, то целевое утверждение согласовано. Если нет, то Пролог переходит к следующему утверждению, голова которого сопоставима с целевым утверждением, и так далее до тех пор, пока целевое утверждение не будет согласовано или не будет доказано, что оно не согласуется с базой данных.
В качестве примера рассмотрим утверждения:
меньше(X.Y) :-
XY, write(X),
write ('меньше, чем'),write(Y).
меньше(Х.У) :-
XY, write(Y),
write ('меньше, 4CM'),write(X).
Целевое утверждение
?- меньше (5, 2).
сопоставляется с головой первого утверждения при Х=5 и У=2. Однако не удается согласовать первый член конъюнкции в теле утверждения X<Y. Значит, Пролог нс может использовать первое утверждение для согласования целевого утверждения меньше(5, 2). Тогда Пролог переходит к следующему утверждению, голова которого сопоставима с целевым утверждением. В нашем случае это второе утверждение. При значениях переменных Х=5 и Y=2 тело утверждения согласуется. Целевое утверждение меньше(5,2) доказано, и Пролог выдает сообщение “2 меньше, чем 5”. Запрос
?-меньше (2, 2).
сопоставляется с головой первого утверждения, но тело утверждения согласовать не удается. Затем происходит сопоставление с головой второго утверждения, но согласовать тело опять-таки оказывается невозможно. Поэтому попытка доказательства целевого утверждения меньше(2, 2) заканчивается неудачей.
Такой процесс согласования целевого утверждения путем прямого продвижения по программе мы называем прямой трассировкой (forward tracking). Даже если целевое утверждение согласовано, с помощью прямой трассировки мы можем попытаться получить другие варианты его доказательства, т.е. вновь согласовать целевое утверждение.
Пролог производит доказательство конъюнкции целевых утверждений слева направо. При этом может встретиться целевое утверждение, согласовать которое не удается. Если такое случается, то происходит смещение влево до тех пор, пока не будет найдено целевое утверждение, которое может быть вновь согласовано, или не будут ис черпаны все предшествующие целевые утверждения. Если слева нет целевых утверждений, то конъюнкцию целевых утверждений согласовать нельзя. Однако, если предшествующее целевое утверждениг может быть согласовано вновь, Пролог возобновляет процесс доказательства целевых утверждений слева направо, начиная со следующего справа целевого утверждения. Описанный процесс смещения влево для повторного согласования целевого утверждения и возвращения вправо носит название механизма возврата.
Пример: задача поиска пути в лабиринте
В качестве примера использования механизма возврата напишем процедуру для поиска пути в лабиринте. Лабиринт представлен фактами вида:
стена(I, J) для позиции в I-м ряду и J-й колонке, где есть стена
отсутств_стена(I, J) для позиции в I-м ряду и J-й колонке, где нет стены
выход (I, J) для позиции в 1-м ряду и J-й колонке, являющейся выходом
Рассмотрим небольшой лабиринт:
| Стена | Стена | Стена | Стена | Стена |
| Стена | Стена | Стена | Стена | |
| Выход | Стена | Стена | Стена | |
| Стена | Стена | Стена | Стена |
Последний ряд лабиринта описывается фактами:
стена(4,1).
стена(4,3).
стена(4,4).
отсутств_стена(4,2).
Если задана исходная позиция, путь к выходу можно найти следующим образом.
Граничное условие:
Если исходная позиция является выходом, то путь найден.
Рекурсивные условия:
Ищем путь из исходной позиции в северном направлении. Если пути нет, идем на юг. Если пути нет, идем на запад. Если нельзя, идем на восток. Если соседняя позиция на севере (юге, западе, востоке) является стеной, то нет смысла искать путь из начальной позиции к выходу. Чтобы не ходить кругами, будем вести список позиций, в которых мы побывали.
Изложенному способу решения задачи соответствует процедура путь: она ищет путь (второй аргумент) к выходу из некоторой позиции (первый аргумент). Третьим аргументом является список позиций, где мы побывали.
/* Терм a(I, J) представляет позицию в
/* I-м ряду и J-й колонке.
/* Нашли путь ?
путь(а(I, J),[а(I, J)], Были) :- выход(I, J).
/* Пытаемся идти на север
путь(а(I, J),[а(I, J) | Р], Были) :-
К is I-1,
можем_идти(a (K, J), Были),
путь(а(I, J) ,Р, [a(K, J) | Были]).
/* Пытаемся идти на юг
путь(а(I, J),[а(I, J) | Р], Были) :-
К is I+1,
можем_идти(a (K, J), Были),
путь(а(I, J) ,Р, [a(K, J) | Были]).
/* Пытаемся идти на запад
путь(а (I, J), [a (I, J) | P], Были) :-
L is J-1,
можем_идти(а(I, L), Были),
путь(а(I, L), Р, [а(I, L)| Были]).
/* Пытаемся идти на восток
путь(а (I, J), [a (I, J) | P], Были) :-
L is J+1,
можем_идти(а(I, L), Были),
путь(а(I, L), Р, [а(I, L)| Были]).
/* в позицию a(I, J) можно попасть при
/* условии, что там нет стены и мы
/* не побывали в ней прежде
можем_идти(а(I, J)), Были) :-
отсутств_стена(I, J),
not (принадлежит (a (I, J), Были)).
Для того чтобы понять, каким образом процедура ищет путь к выходу, рассмотрим процесс согласования запроса с описанием лабиринта, описанного выше:
?-путь(а(4,2), Р, [а(4.2)]).
Выходом из лабиринта является позиция выход (3,1).
Выбор первого утверждения не приводит к согласованию целевого утверждения, поскольку а (4,2) - не выход. Во втором утверждении делается попытка найти путь в северном направлении, т.е. согласовать целевое утверждение
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]).
Целевое утверждение не удается согласовать с первым утверждением
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)])
так как а (3,2) не является выходом. Во втором утверждении предпринимается попытка найти путь, двигаясь на север, т.е. согласовать целевое утверждение
путь(а(2,2), РЗ, [а(2, 2), а(3, 2), а(4, 2)]).
Ни одно из утверждений не может согласовать
путь(а(2, 2), РЗ, [а(2, 2), а(3, 2), а(4, 2)]).
Первое утверждение - потому, что а (2, 2) не является выходом, второе - потому, что северная позиция является стеной, третье утверждение - потому, что в южной позиции мы уже побывали, а четвертое и пятое утверждения - потому, что западная и восточная границы - это стены.
Неудача в согласовании
путь(а(2, 2), РЗ, [а(2, 2), а(3, 2), а(4, 2)])
заставляет Пролог-систему вернуться в ту точку, где было выбрано второе утверждение при попытке согласовать
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]).
Решение пересматривается и выбирается третье утверждение.
В третьем утверждении осуществляется попытка найти путь, двигаясь на юг, но она оказывается неудачной, поскольку мы уже побывали в позиции а (4, 2). Тогда, чтобы согласовать
путь(а(3, 2), Р2, [а(3, 2), а(4, 2)]),
выбирается четвертое утверждение. Мы успешно находим путь, двигаясь в западном направлении к позиции а(3,1), которая и является выходом. Рекурсия сворачивается, и в результате получается путь
Р=[а(4, 2),а(3, 2), а(3,1)]
другие решения(да/нет)? да
Других решений нет
Альтернативный путь
[a(4,2), a(3,2), a(2,2), a(3,2), a(3,1)]
мы получить не можем, потому что не разрешается дважды бывать в одной и той же позиции.
Описанная процедура не обязательно находит кратчайший путь к выходу. Кратчайший путь можно найти, генерируя альтернативные пути с помощью вызова состояния неудачи и запоминая кратчайший из них.